いろいろ level curves of a function calculator 926447

My Partial Derivatives course https//wwwkristakingmathcom/partialderivativescourseIn this video we're talking about how to sketch the level curves ofWith this ability, you could flow across continuouslyspaced level curves12) Higher Order Example 1;

Hgm4 14 Review 71 Gradients Etc Pg Query

Level curves of a function calculator

Level curves of a function calculator-11) Utility Function Example; The whole point of a "level" curve is that the function stays at the same "level", ie the same value The level curve is f(x,y)= yx 2 y 2 = 3 Yes, your tangent line is correct

The Modulus Function Mathematics Learning And Technology

Double checking my own approximation to the function for a solution to the inf circular potential well in QM 4 1426 years old level / Highschool/ University/ Grad student / Useful /10) Level Indifference Curve;The procedure to use the area between the two curves calculator is as follows Step 1 Enter the smaller function, larger function and the limit values in the given input fields Step 2 Now click the button "Calculate Area" to get the output Step 3 Finally, the area between the two curves will be displayed in the new window

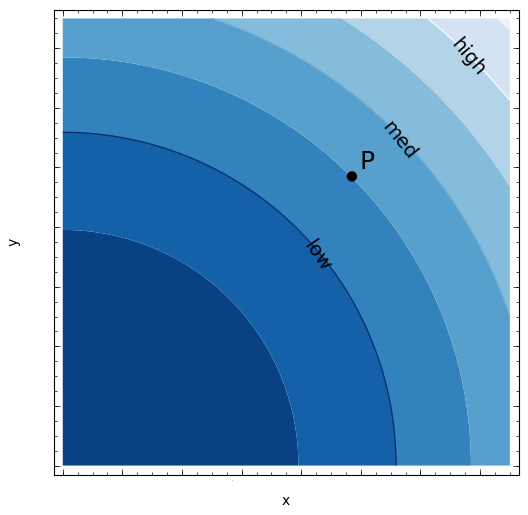
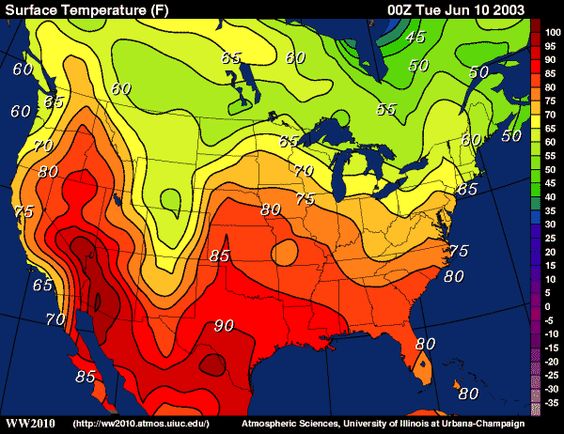
 Section 15 Functions of Several Variables In this section we want to go over some of the basic ideas about functions of more than one variable First, remember that graphs of functions of two variables, z = f (x,y) z = f ( x, y) are surfaces in three dimensional space For example, here is the graph of z =2x2 2y2 −4 z = 2 x 2 2 y 2 − 4Level curves Level curves for a function z = f ( x, y) D ⊆ R 2 → R the level curve of value c is the curve C in D ⊆ R 2 on which f C = c Notice the critical difference between a level curve C of value c and the trace on the plane z = c a level curve C always lies in the x y plane, and is the set C of points in the x y plane onBy default this expression is x^2 y^2 So if x = 2, and y = 2, z will equal 4 4 = 0 Try hovering over the point (2,2) above You should see in the sidebar that the (x,y,z) indicator displays (2,2,0) So, that explains why we see a contour line along the line

Add a Calculator application to a TINspire document and enter the following Solving z = f(x;y) succeeded and there are two solutions which can be used to create lists of functions to plot the level curves Step 2 Graph z = f(x;y) and use the menu item Trace zTrace to determine the14) Calculator Example ;Answer (1 of 5) A level curve can be drawn for function of two variable ,for function of three variable we have level surface A level curve of a function is curve of points where function have constant values,level curve is simply a cross section of graph of function

The 9 Best Graphing Calculators Of 21

Practice Quiz 5 Multivariable And Vector Calculus Math 275 Docsity

Level curves Author Siamak The level curves of two functions and Blue represents and red represents Since and are both harmonic and is a harmonic conjugate of , the level curves of and intersect each other at right anglesTo find a normal vector to a surface, view that surface as a level set of some function A normal vector to the implicitly defined surface is Level curves and surfaces We identify the surface as the level curve of the value for Definition of the gradient The gradient of is Evaluating at , we get A level curve of a function f(x,y) is a set of points (x,y) in the plane such that f(x,y)=c for a fixed value c Example 5 The level curves of f(x,y) = x 2 y 2 are curves of the form x 2 y 2 =c for different choices of c These are circles of

Level Sets Ximera

Level Curve Calculator Online Discount Shop For Electronics Apparel Toys Books Games Computers Shoes Jewelry Watches Baby Products Sports Outdoors Office Products Bed Bath Furniture Tools Hardware Automotive Parts

 Level curve calculator in Description DgFlick Edit Xpress STD DgFlick Edit Xpress is an easy to use photo correction tool You get basic editing tools like BCG, RGB, Level, Curve and advanced editing tools like Lasso, Chroma, Touchup, Highlighter, etc Batch editing feature lets you color correct 1000s of the photos in a single clickThe function z = ¨ xy ¨ In17= Plot3D@Abs@xyD, 8x,1, 1 30, Mesh> False, AxesLabel> 8"x","y","z"02) Saddle Points and Example 1;

Fx Cg50 Graphic Models School Lab Calculators Casio

Level Curve Calculator Online Discount Shop For Electronics Apparel Toys Books Games Computers Shoes Jewelry Watches Baby Products Sports Outdoors Office Products Bed Bath Furniture Tools Hardware Automotive Parts

The calculator will find the tangent line to the explicit, polar, parametric and implicit curve at the given point, with steps shown It can handle horizontal and vertical tangent lines as well The tangent line is perpendicular to the normal lineThese curves are the straight lines in the figure On 6x8y=C, f(x,y)=C The value of C is listed on each level curve in the figure As the plot shows, the function of f(x,y) takes on values between 10 and 10 for points on the circle Hence, the maximum is 10 and the minimum is 10 Note that the maximum and minimum occur at points where theOne way to collapse the graph of a scalarvalued function of two variables into a twodimensional plot is through level curves A level curve of a function f ( x, y) is the curve of points ( x, y) where f ( x, y) is some constant value A level curve is simply a cross section of the graph of z = f ( x, y) taken at a constant value, say z = c

2

The Difference Between Levels And Curves In Photoshop Petapixel

Gradients and Level Curves Recall that if a curve is defined parametrically by the function pair then the vector is tangent to the curve for every value of in the domain Now let's assume is a differentiable function of and is in its domain Let's suppose further that and for some value of and consider the level curve Define and calculate on the level curveReturning to the function g (x, y) = 9 − x 2 − y 2, g (x, y) = 9 − x 2 − y 2, we can determine the level curves of this function The range of g g is the closed interval 0, 3 0, 3 First, we choose any number in this closed interval—say, c = 2 c = 2 The level curve corresponding to c = 2 c = 2 is described by the equation Cost Function Formula The following is the typical cost function associated with producing goods C (x) = FC x * VC Where C (x) is the total cost at x number of units FC is the fixed cost x is the total number of units VC is the average variable cost per unit This is considered the most standard cost function, but a cost function can be

Best Graphing Calculators In Depth Buyer S Guide

Sample Size Calculation From Two Roc Curves With A Different Ratio Of Cases To Controls Than Sample Data Stack Overflow

13) Higher Order Example 2;05) Level Curves / Contours; These level curves and gradient vector fields are slowly building an outline of a surface in \( \mathbb{R}^3\) However, we are still lacking a way of connecting the curves and the arrows How would one follow the vectors to get from one level curve to the next?

What Grade Level Math Do You Need A Graphing Calculator For Quora

Advanced Earth Curvature Calculator

GRADIENTS AND LEVEL CURVES There is a close relationship between level curves (also called contour curves or isolines) and the gradient vectors of a curve Indeed, the two are everywhere perpendicular This handout is going to explore the relationship between isolines and gradients to help us understand the shape of functions inFree piecewise functions calculator explore piecewise function domain, range, intercepts, extreme points and asymptotes stepbystep This website uses cookies to ensure you get the best experience By using this website, you agree to our Cookie PolicyThe formula for calculating the length of a curve is given as L = ∫ a b 1 ( d y d x) 2 d x Where L is the length of the function y = f (x) on the x interval a, b and is the derivative of the function y = f (x) with respect to x The arc length formula is derived from the methodology of approximating the length of a curve

Ccp Margin Calculation

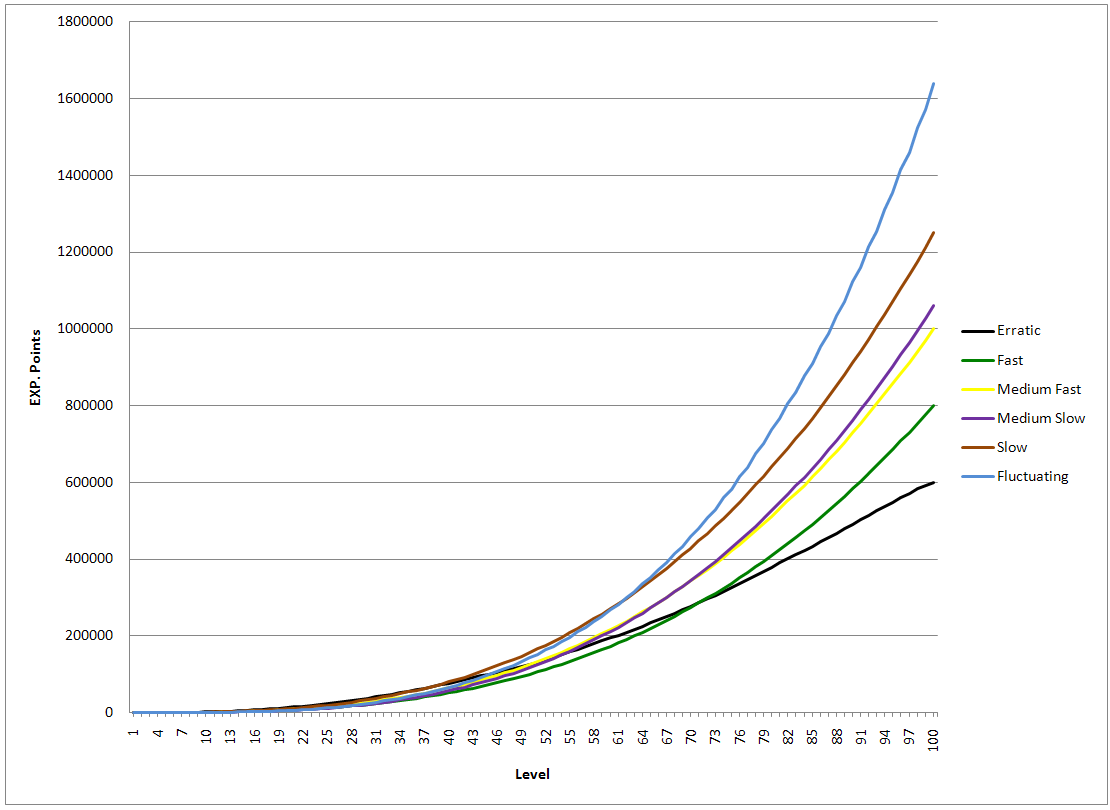
Experience Bulbapedia The Community Driven Pokemon Encyclopedia

Level surfaces For a function $w=f(x,\,y,\,z) \, U \,\subseteq\, {\mathbb R}^3 \to {\mathbb R}$ the level surface of value $c$ is the surface $S$ in $U \subseteqIt would be nice to be able to fit the curve, specifically through the origin (y=Ax^2Bx regression) 2339 years old level / Highschool/ University/ Grad student / Very / Purpose of use Determine coefficients of a virial expansion quadratic equation by fitting data to function 10 2137 30 years old levelCurve sketching is a calculation to find all the characteristic points of a function, eg roots, yaxisintercept, maximum and minimum turning points, inflection points How to get those points?

Tangent Plane Calculator Find Equation Step By Step

How Do You Sketch Level Curves Of Multivariable Functions Vector Calculus 3 Youtube

 I am being asked to calculate level curves for the following equation f(x,y)=e^(2x^22y^2) but I do not know where to start Any adviceLevel Curves Def If f is a function of two variables with domain D, then the graph of f is {(x,y,z) ∈ R3 z = f(x,y) } for (x,y) ∈ D Def The level curves of a function f(x,y)are the curves in the plane with equations f(x,y)= kwhere is a constant in the range of f The contour curves are the corresponding curves on the surface, theDefinition The level curves of a function f of two variables are the curves with equations f (x,y) = k, where k is a constant (in the range of f ) A level curve f (x,y) = k is the set of all points in the domain of f at which f takes on a given value k In other words, it shows where the graph of f

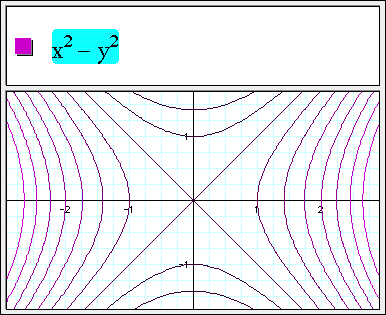
Graphing Calculator Contour Plot

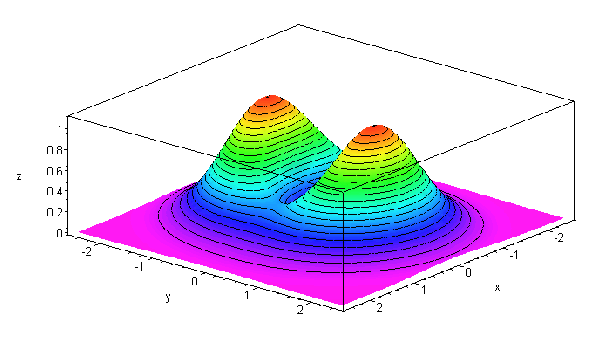
Level Curves

The curve $100=2x2y$ can be thought of as a level curve of the function $2x2y$;You have a function f R 2 → R The level curves of f is the set { ( x, y) ∈ R 2 f ( x, y) = K, K ∈ R } So, in order to find the level curves of your function, just set it equal to a constant K, and try different values of K For instance f ( x, y) = ( x 2 y 2 − 1) ( 2 x y − 1) = K Now, test values foe K, say K = − 1, −By calculating derivatives Then you set the function as well as the derivative equal to zero Roots are solutions of the equation

Problem Of Level Curves Leading Lesson

Level Sets Ximera

Get the free "Level Curves" widget for your website, blog, Wordpress, Blogger, or iGoogle Find more Mathematics widgets in WolframAlpha Mathematics Stack Exchange is a question and answer site for people studying math at any level and professionals in related fields It only takes a minute to sign upThis tool graphs z = f(x,y) mathematical functions in 3D It is more of a tour than a tool All functions can be set different boundaries for x, y, and z, to maximize your viewing enjoyment This tool looks really great with a very high detail level, but you may find it more comfortable to use less detail if you want to spin the model

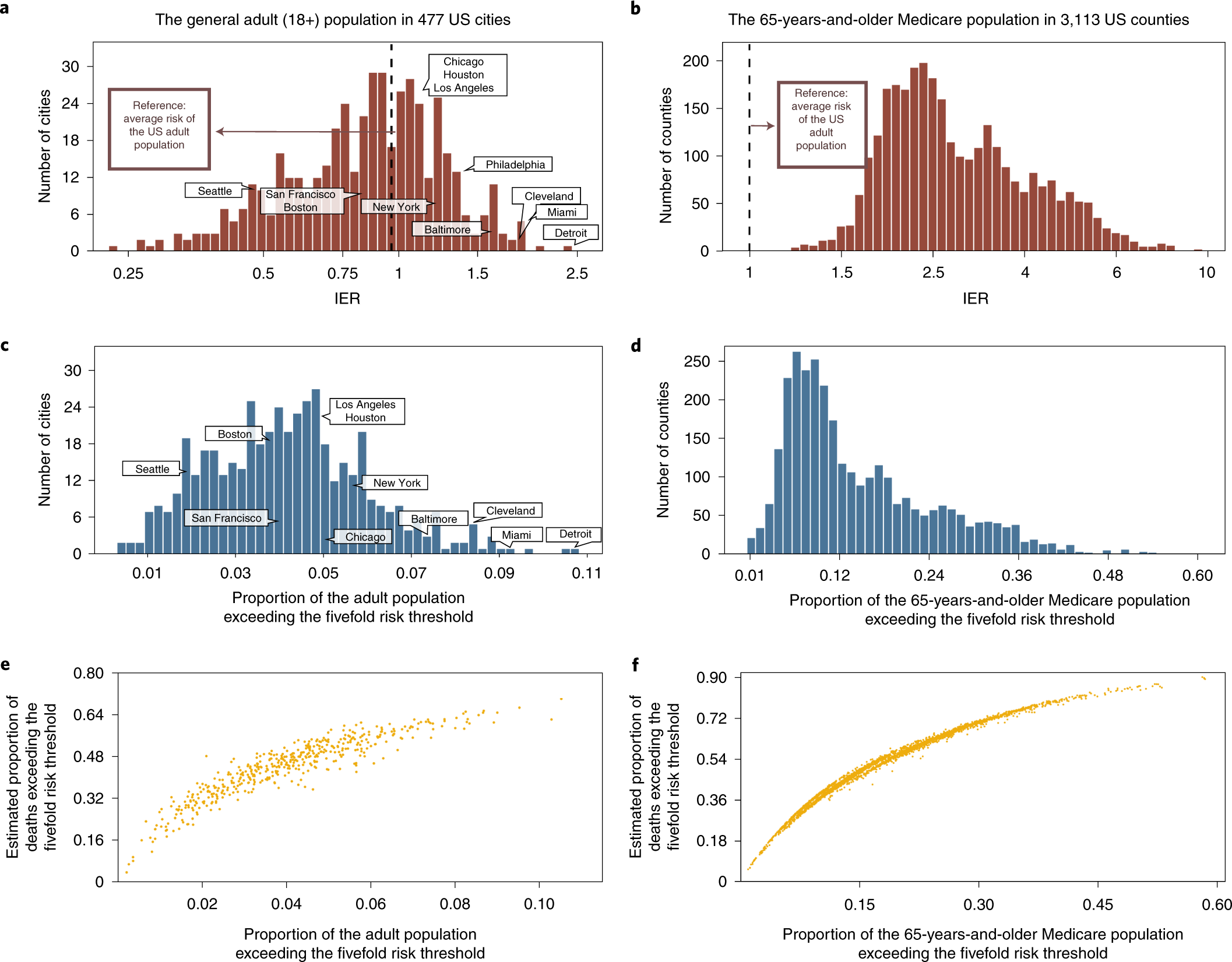
Individual And Community Level Risk For Covid 19 Mortality In The United States Nature Medicine

Level Curves Geogebra

1 Level Surfaces 2 If one of the Arguments is time we can animate ie w = f(x,y,t) Level Surfaces Given w = f(x,y,z) then a level surface is obtained by considering w = c = f(x,y,z) The interpretation being that on a level surface f has the same value at every pt For example f could represent the temperature at each pt in 3spacePerpendicular to the level set curve at the point (1;1), where the gradient was evaluated You can also note that the gradient is pointing in the direction of steepest ascent of z(x;y)8 16 Level Curves and Feasible Region At optimality the level curve of the objective function is tangent to the binding constraints11A free graphing calculator graph function, examine intersection points, find maximum and minimum and much more This website uses cookies to ensure you get the best experience By using this website, you agree to our Cookie Policy

Gradients And Level Curves

Iso 226 Normal Equal Loudness Level Contour Calculator

 How to Find the Level Curves of a Function Calculus 3 How to Find the Level Curves of a Function Calculus 307) Cobb Douglas Production Function;Visualizing level curves Author Braxton Carrigan Topic Functions This allows students to see level curves drawn simultaneously with the 3D image of the intersection of the plane and the curve The only issue the user should be aware of is that the 2variable function must be polynomial in both x and y

13 Best Graphing Calculators To Enjoy Today Buyer S Guide Architecture Lab

Solved Describe The Level Curves Of The Function Z 8 2x 7y Chegg Com

If the calculator did not compute something or you have identified an error, or you have a suggestion/feedback, please write it in the comments below Your input find the area between the following curves $$$ y = x^{2} $$$ , $$$ y = \sqrt{x} $$$ on the interval $$$ \left(\infty, \infty\right) $$$Figure 16 shows both sets of level curves on a single graph We are interested in those points where two level curves are tangent—but there are many such points, in fact an infinite number, as we've only shown a few of the level curvesLevel Curve Grapher Enter a function f (x,y) Enter a value of c Enter a value of c Enter a value of c Enter a value of c Submit

Functions Of Several Variables

Hw2 Sol Pdf Pdf Acceleration Mathematical Objects

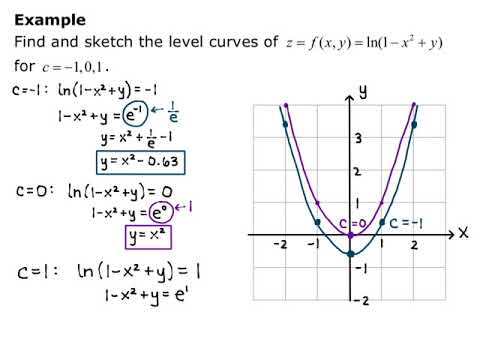
For the following exercises, find the level curves of each function at the indicated value of c to visualize the given function h(x,y)In(x2y2);c=1,0,1 a, For the following exercises, find the vertical traces of the functions at the indicated valuesLevel Curves So far we have two methods for visualizing functions arrow diagrams and graphs A third method, borrowed from mapmakers, is a contour map on which points of constant elevation are joined to form contour curves, or level curves A level curve f (x, y) = k is the set of all points in the domain of f at which f takes on a given value k

1

The 9 Best Graphing Calculators Of 21

Level Curves Geogebra

Section 13 1 Level Curves Youtube

Data Logging And Cooling Curves Casioed

Sones Phons Loudness Decibel Sone 0 2 0 3 0 4 0 5 0 6 Define Sone Rating Conversion Db Level Dba Phon Phone Volume Intensity Calculator Db Dba And Sone Relate Fan

Level Surfaces

Slope Of A Level Curve Youtube

Dc Motor Tutorial Motor Calculations For Coreless Brush Dc Motors

The Modulus Function Mathematics Learning And Technology

Quick And Dirty Procedure To Calculate

Level Curves And Cross Sections Maple Help

Level Curves Of Function At Z 0 Mathematics Stack Exchange

Damage Calculator

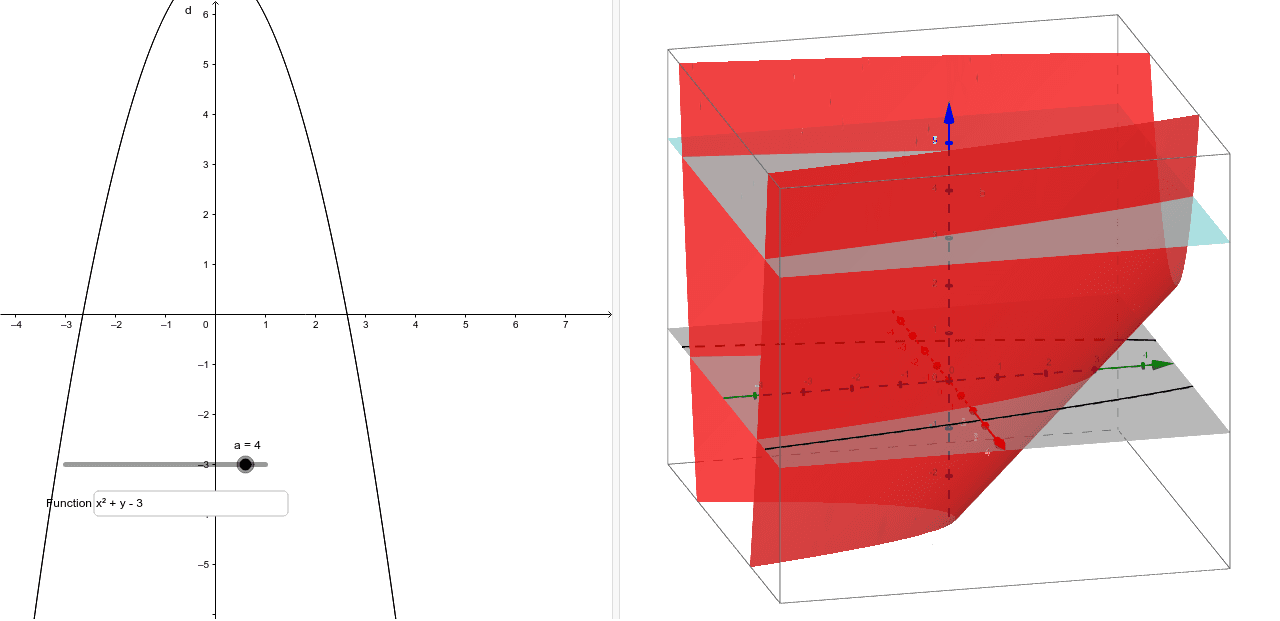
Visualizing Level Curves Geogebra

Csun Edu

The Modulus Function Mathematics Learning And Technology

Cable Sag Error Catenary Curve Effect Calculator

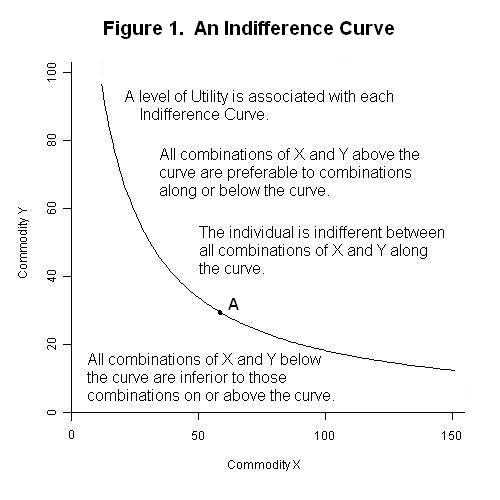
Indifference Curves

The Gradient And Directional Derivative

Math 15 Lecture 7 Level Curves And Contour Plots Oneclass

Casio 9860gii

People Whitman Edu

Level Curves

Level Sets Ximera

Best Free Online Graphing Calculator 19 Ti 84 Plus 3d Download

Why Is The Gradient Related To The Normal Vector To A Surface Continuous Everywhere But Differentiable Nowhere

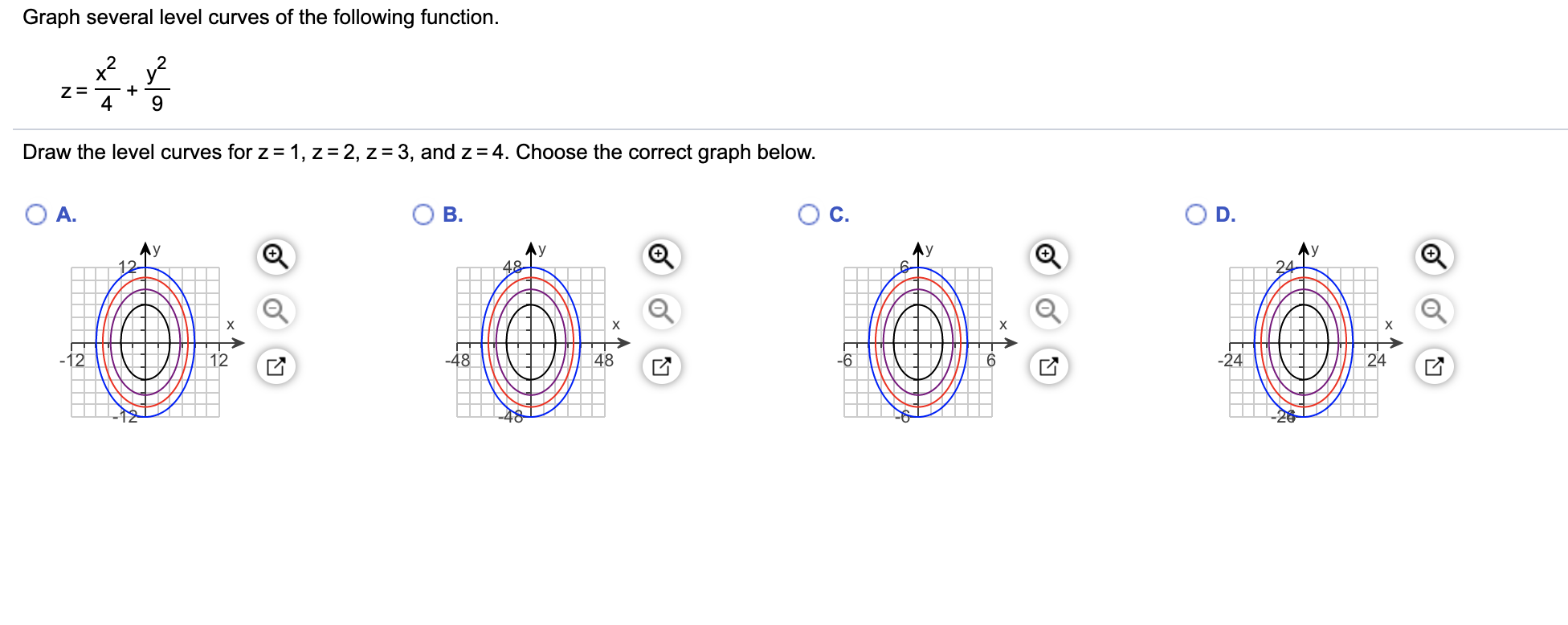
Solved Graph Several Level Curves Of The Following Function Chegg Com

Top 7 Uses For A Graphing Calculator Hp Tech Takes

3

Level Surfaces

Level Curves And Contour Plots Mathonline

Math 148 Exam Iii Practice Problems

Lagrange Multipliers

Level Curves Geogebra

Graphical Calculators For Continuous Distributions

Area Between Two Curves Calculator Find Area Between Curves

Global And European Sea Level Rise European Environment Agency

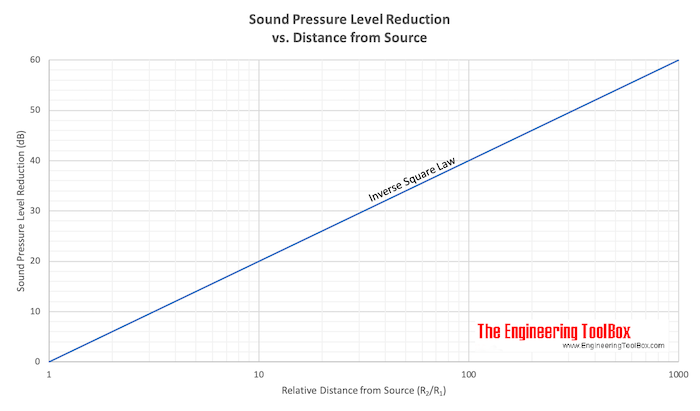
Sound Propagation The Inverse Square Law

Hgm4 14 Review 71 Gradients Etc Pg Query

Level Sets Math Insight

Level Curves And Implicit Differentiation Studocu

Online Area Calculator Between Two Crossed Curves

Answered Exercise Ii Contour Maps For Each Of Bartleby

Solved Sketch The Graph Of Each Function By Computing Some Level Curves And Sections F X Y X Y

Desmos Accessibility

1

Mechanical Power Calculation Which Includes The Resistive Properties Download Scientific Diagram

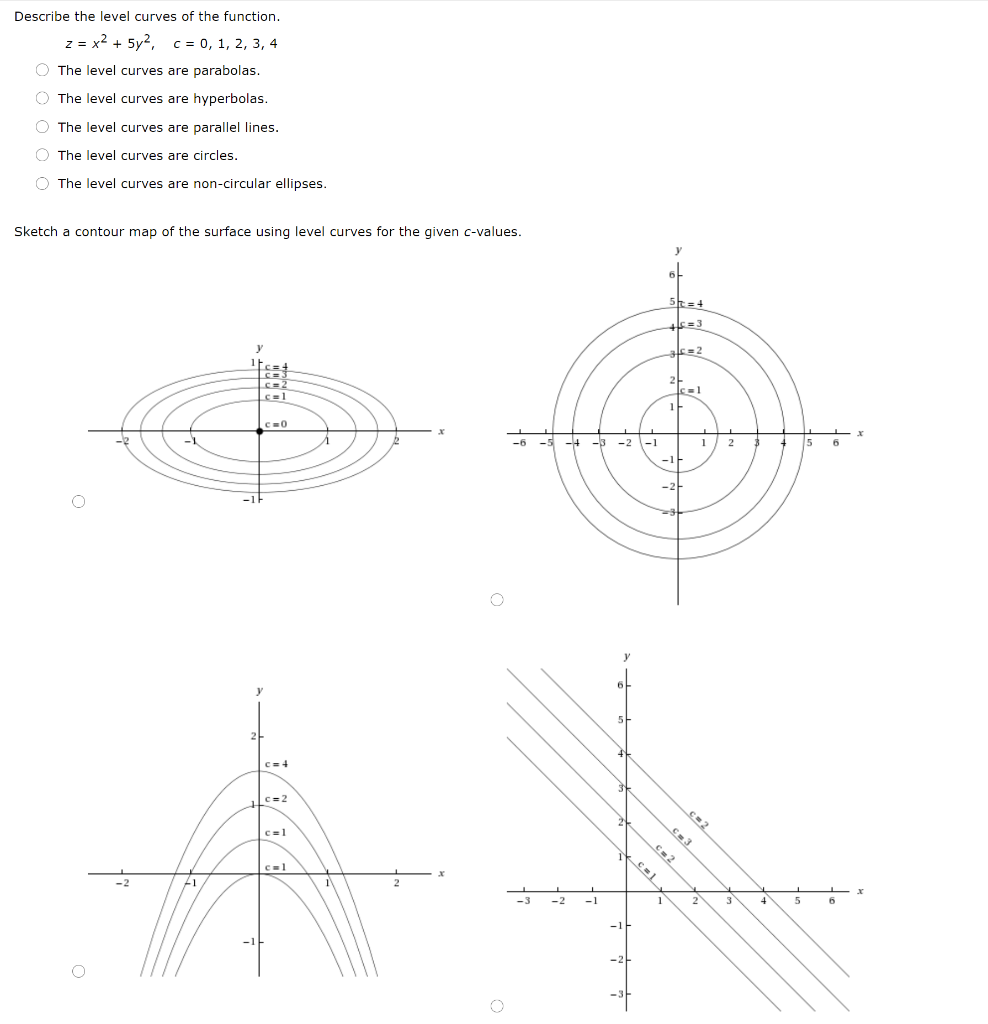
Solved Describe The Level Curves Of The Function Z X2 Chegg Com

Graphing Calculators Ideal To Ease Complex Mathematical Equations Most Searched Products Times Of India

Calculus Iii Functions Of Several Variables

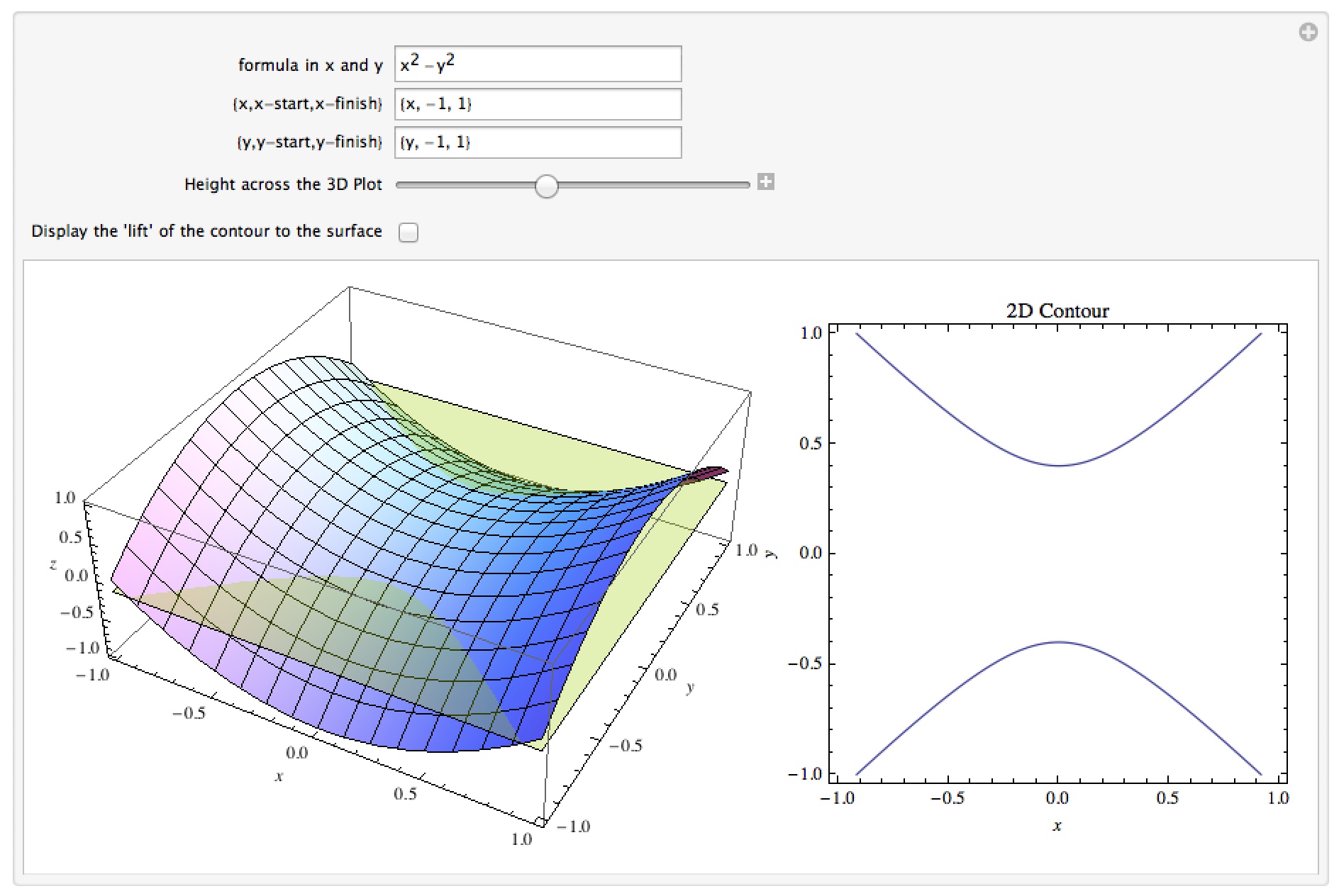
Dr Moretti S Mathematica Notebooks Calculus 3

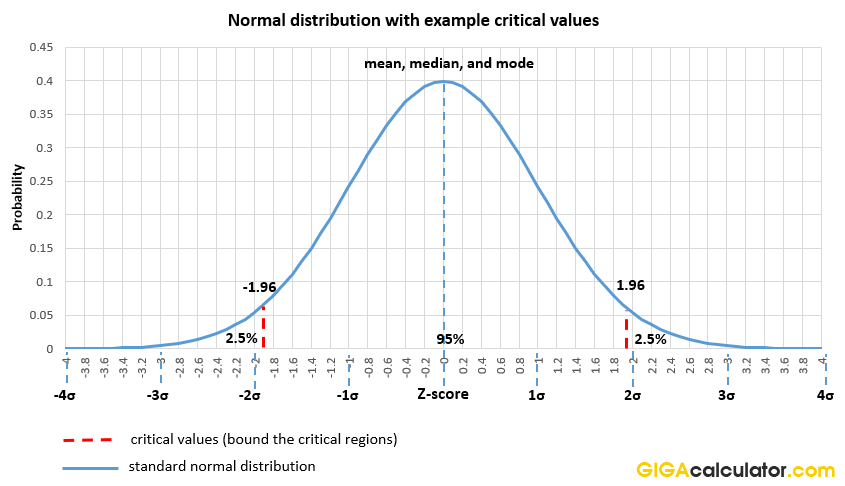
Normal Distribution Calculator With Formulas Definitions

Level Curves

Solved Sketch The Level Curves Of The Function G X Y Chegg Com

Level Curves Curves Level Stvincent Glogster Edu Interactive Multimedia Posters

How To Sketch Level Curves Youtube

Relief Functions And Level Curves

Integral Calculator Integrate With Wolfram Alpha

Normal Distribution Calculator High Accuracy Calculation

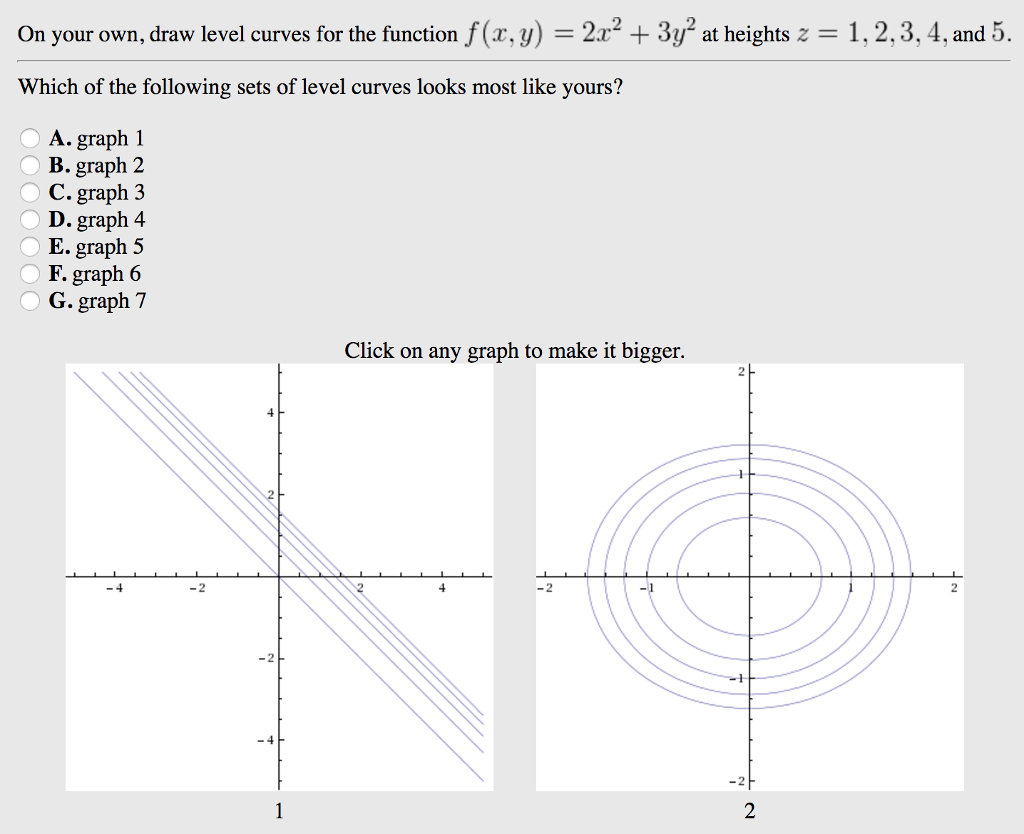
Level Curve Calculator Online Discount Shop For Electronics Apparel Toys Books Games Computers Shoes Jewelry Watches Baby Products Sports Outdoors Office Products Bed Bath Furniture Tools Hardware Automotive Parts

Approximating Limits On A Graphing Calculator Video Lesson Transcript Study Com

M1c Exam1 Notes F14

Level Curves And Contour Plots Mathonline

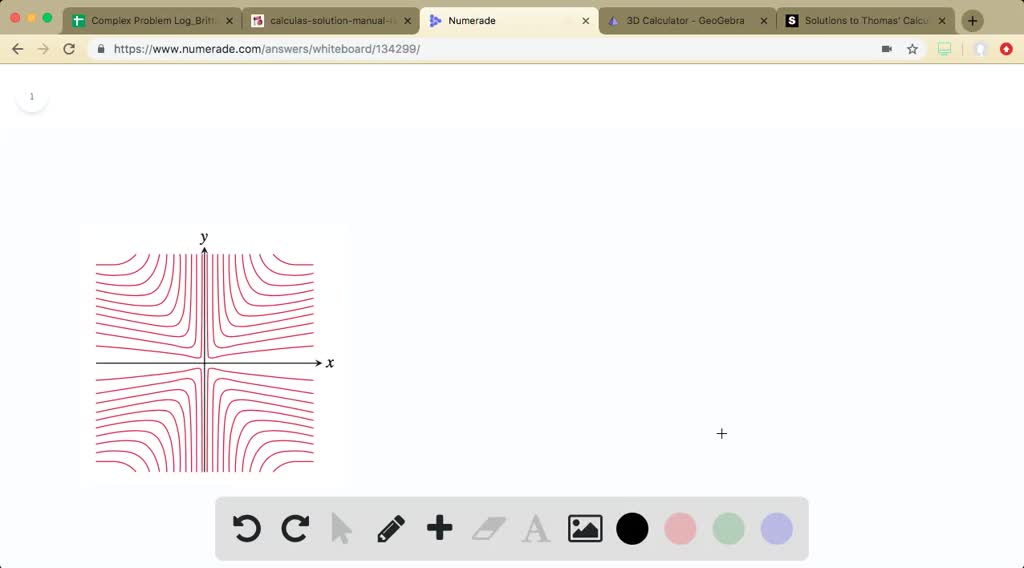
Solved Exercises 31 36 Show Level Curves For Six Functions The Graphs Of These Functions Are Given On The Next Page Items A F As Are Their Equations Items G L Match Each Set Of Level

A Weighting Wikipedia

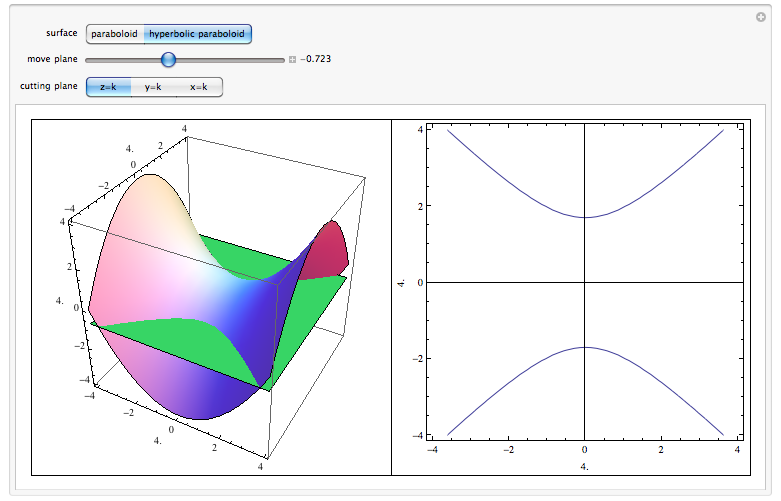
Surfaces And Traces

How Do You Sketch Level Curves Of Multivariable Functions Krista King Math Online Math Tutor

Casio Fx 991ex Classwiz Non Programmable Scientific Calculator 552 Functions With Menu Driven Interface Amazon In Office Products

Calculus Iii Functions Of Several Variables

1

Solved Describe The Level Curves Of The Function Z X2 Chegg Com

Solved In Exercise A Use A Computer Or Calculator To Plot The Graph Of The Function F And B Plot Some Level Curves Of F And Compare Them With The Graph Obtained In

Level Set Examples Math Insight

Calculus Iii Functions Of Several Variables

Level Sets Math Insight